Huffman encoding and decoding by java

Abstract: Huffman coding has been widely used in various applications in everyday life. In this article, we will describe the method of Huffman coding and decoding implemented in Java as the core of our discussion.

Huffman coding, also known as Huffman encoding, is a type of variable-length coding (VLC) method. It was introduced by David Huffman in 1952. This technique constructs codewords with the shortest average length based on the probability of occurrence of each character, making it an optimal encoding method. It is often referred to as Huffman encoding or sometimes called Hoffmann coding.

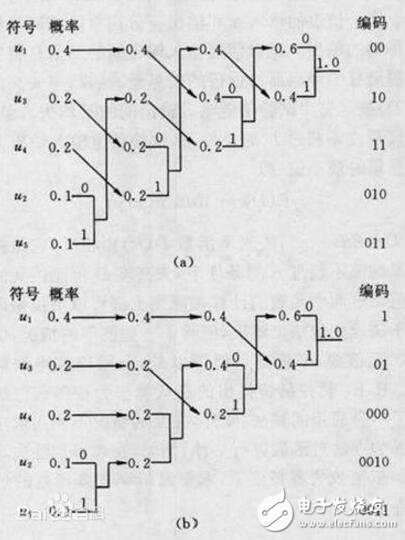
Consider a source that generates five symbols: u1, u2, u3, u4, and u5, with probabilities P1 = 0.4, P2 = 0.1, P3 = P4 = 0.2, and P5 = 0.1. The process begins by sorting these symbols based on their probabilities from highest to lowest. Then, two symbols with the lowest probabilities are combined into a subtree, assigning '0' to one branch and '1' to the other. The combined probability is then reinserted into the list, and the process repeats until only one node remains. The resulting binary tree provides the unique code for each symbol. Although the average code length may be the same, different codes can be assigned due to multiple paths during the merging process. This non-uniqueness arises because when multiple nodes have the same probability, the order of merging can vary, affecting the final code lengths. Generally, placing the merged node at the top of the list helps minimize the variance in code lengths and results in more balanced codes.

The Huffman code ensures that no codeword is a prefix of another, which allows the receiver to decode the message without additional separation symbols, as long as the transmission is error-free. This property makes Huffman coding efficient and widely applicable in data compression.

In practical applications, challenges include statistical matching for small symbol sets, such as black (1) and white (0) in fax machines. These systems use extended symbol sets based on run-lengths—sequences of the same symbol. According to CCITT standards, runs up to 1728 different lengths must be considered, leading to high memory requirements. To reduce complexity, runs longer than 64 are encoded using a primary code and a base code. This modified Huffman coding is commonly used in fax machines to improve efficiency and reduce storage needs.

Huffman encoding involves converting a string into a binary representation based on the frequency of characters. During encoding, each character is assigned a unique binary code, while decoding requires knowing these codes to reconstruct the original string.

According to the algorithm described in "Multimedia Technology Tutorial" by Li Zeian, the steps for Huffman coding are as follows:

• Initialization: Create a list of nodes sorted by frequency.
• Repeat until only one node remains:
• Select the two nodes with the lowest frequency.
• Create a parent node with these two as children, and assign the sum of their frequencies.
• Insert the parent node back into the list and remove the children.
• Assign a code to each leaf node based on the path from the root.

My implementation follows this algorithm. I read the English version of the book since the Chinese electronic version was unavailable, but the content was straightforward.

Decoding, although simpler, relies on the encoding information generated during the encoding process. This includes the mapping between characters and their corresponding codes. Without this information, decoding would not be possible.

Here is the Java code implementing Huffman encoding and decoding:

This implementation defines classes for nodes, data, and encoding results. It includes methods to build the Huffman tree, generate codes, and perform both encoding and decoding operations. The test cases verify the functionality of the algorithm with sample strings.

Fiber Reinforced Composite Material

Fiber Reinforced Composite Material,Hard Composite Graphite Fiber Felt,Vacuum Furnace Heat Insulation Ring,Insulation Material For Vacuum Furnace

HuNan MTR New Material Technology Co.,Ltd , https://www.hnmtr.com